Что такое симплекс
Симплекс-метод — Википедия
- Не путать с «симплекс-методом» — методом оптимизации произвольной функции. См. Метод Нелдера — Мида
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.
Сущность метода: построение базисных решений, на которых монотонно убывает линейный функционал, до ситуации, когда выполняются необходимые условия локальной оптимальности.
В работе Л. В. Канторовича «Математические методы организации и планирования производства» (1939) были впервые изложены принципы новой отрасли математики, которая позднее получила название линейного программирования.[1]
Исторически общая задача линейного программирования была впервые поставлена в 1947 году Джорджем Бернардом Данцигом, Маршаллом Вудом и их сотрудниками в департаменте военно-воздушных сил США. В то время эта группа занималась исследованием возможности использования математических и смежных с ними методов для военных задач и проблем планирования. В дальнейшем для развития этих идей в ВВС была организована исследовательская группа под названием Project SCOOP. Первое успешное решение задачи линейного программирования на ЭВМ SEAC было проведено в январе 1952 года [2].
Переход от одной вершины к другойЗадача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.
Заметим, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый выпуклый многогранник (возможно, бесконечный), называемый также полиэдральным комплексом. Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.
Последовательность вычислений симплекс-методом можно разделить на две основные фазы:
- нахождение исходной вершины множества допустимых решений,
- последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.
При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.
Усиленная постановка задачи[править | править код]
Рассмотрим следующую задачу линейного программирования:
- cTx→max,Ax⩽b,x⩾0,b⩾0.{\displaystyle c^{T}x\to \max ,Ax\leqslant b,x\geqslant 0,b\geqslant 0.}
Теперь поставим эту задачу в эквивалентной усиленной форме. Необходимо максимизировать Z, где:
- [1−cT00AE][Zxxs]=[0b],x,xs⩾0{\displaystyle {\begin{bmatrix}1&-c^{T}&0\\0&A&E\end{bmatrix}}{\begin{bmatrix}Z\\x\\x_{s}\end{bmatrix}}={\begin{bmatrix}0\\b\end{bmatrix}},x,x_{s}\geqslant 0}
Здесь x — переменные из исходного линейного функционала, xs — новые переменные, дополняющие старые таким образом, что неравенство переходит в равенство, c — коэффициенты исходного линейного функционала, Z — переменная, которую необходимо максимизировать. Полупространства x⩾0{\displaystyle x\geqslant 0} и xs⩾0{\displaystyle x_{s}\geqslant 0} в пересечении образуют многогранник, представляющий множество допустимых решений. Разница между числом переменных и уравнений даёт нам число степеней свободы. Проще говоря, если мы рассматриваем вершину многогранника, то это число рёбер, по которым мы можем продолжать движение. Тогда мы можем присвоить этому числу переменных значение 0 и назвать их «небазисными». Остальные переменные при этом будут вычисляться однозначно и называться «базисными». Сам же набор этих переменных называется базисом. Полученная точка будет вершиной в пересечении соответствующих небазисным переменным гиперплоскостей. Для того, чтобы найти т. н. начальное допустимое решение (вершину, из которой мы начнём движение), присвоим всем изначальным переменным x значение 0 и будем их считать небазисными, а все новые будем считать базисными. При этом начальное допустимое решение вычисляется однозначно : xsi=bi{\displaystyle \mathbf {x} _{si}=\mathbf {b} _{i}}.
Алгоритм[править | править код]
Теперь приведём шаги алгоритма. На каждом шаге мы будем менять множества базисных и небазисных векторов (двигаться по рёбрам), и матрица будет иметь следующий вид:
- [1cBTB−1A−cTcBTB−10B−1AB−1][Zxxs]=[cBTB−1bB−1b],{\displaystyle {\begin{bmatrix}1&c_{B}^{T}B^{-1}A-c^{T}&c_{B}^{T}B^{-1}\\0&B^{-1}A&B^{-1}\end{bmatrix}}{\begin{bmatrix}Z\\x\\x_{s}\end{bmatrix}}={\begin{bmatrix}c_{B}^{T}B^{-1}b\\B^{-1}b\end{bmatrix}},}
где cB{\displaystyle c_{B}} — коэффициенты вектора c{\displaystyle c}, соответствующие базисным переменным (переменным xs{\displaystyle x_{s}} соответствуют 0), B{\displaystyle B} — столбцы [AE]{\displaystyle [\mathbf {A} \mathbf {E} ]}, соответствующие базисным переменным. Матрицу, образованную оставшимися столбцами обозначим D{\displaystyle D}. Почему матрица будет иметь такой вид поясним в описании шагов алгоритма.
Первый шаг.
Выбираем начальное допустимое значение, как указано выше. На первом шаге B{\displaystyle B} — единичная матрица, так как базисными переменными являются xs{\displaystyle x_{s}}. cB{\displaystyle c_{B}} — нулевой вектор по тем же причинам.
Второй шаг
Покажем, что в выражении (cBTB−1A−cT)x+(cBTB−1)xs{\displaystyle (c_{B}^{T}B^{-1}A-c^{T})x+(c_{B}^{T}B^{-1})x_{s}} только небазисные переменные имеют ненулевой коэффициент. Заметим, что из выражения Ax+xs=b{\displaystyle Ax+x_{s}=b} базисные переменные однозначно выражаются через небазисные, так как число базисных переменных равно числу уравнений. Пусть x′{\displaystyle x'} — базисные, а x″{\displaystyle x''} — небазисные переменные на данной итерации. Уравнение Ax+xs=b{\displaystyle Ax+x_{s}=b} можно переписать, как Bx′+Dx″=b{\displaystyle Bx'+Dx''=b}. Умножим его на B−1{\displaystyle B^{-1}} слева: x′+B−1Dx″=B−1b{\displaystyle x'+B^{-1}Dx''=B^{-1}b}. Таким образом мы выразили базисные переменные через небазисные, и в выражении B−1Ax+B−1xs{\displaystyle B^{-1}Ax+B^{-1}x_{s}}, эквивалентному левой части равенства, все базисные переменные имеют единичные коэффициенты. Поэтому, если прибавить к равенству Z−cTx=0{\displaystyle Z-c^{T}x=0} равенство cBTB−1Ax+cBTB−1xs{\displaystyle c_{B}^{T}B^{-1}Ax+c_{B}^{T}B^{-1}x_{s}}, то в полученном равенстве все базисные переменные будут иметь нулевой коэффициент — все базисные переменные вида x сократятся, а базисные переменные вида xs не войдут в выражение cBTB−1xs{\displaystyle c_{B}^{T}B^{-1}x_{s}}.
Выберем ребро, по которому мы будем перемещаться. Поскольку мы хотим максимизировать Z, то необходимо выбрать переменную, которая будет более всех уменьшать выражение
(cBTB−1A−cT)x+(cBTB−1)xs{\displaystyle (c_{B}^{T}B^{-1}A-c^{T})x+(c_{B}^{T}B^{-1})x_{s}}.
Для этого выберем переменную, которая имеет наибольший по модулю отрицательный коэффициент[3]. Если таких переменных нет, то есть все коэффициенты этого выражения неотрицательны, то мы пришли в искомую вершину и нашли оптимальное решение. В противном случае начнём увеличивать эту небазисную переменную, то есть перемещаться по соответствующему ей ребру. Эту переменную назовём входящей.
Третий шаг
Теперь необходимо понять, какая базисная переменная первой обратится в ноль по мере увеличения входящей переменной. Для этого достаточно рассмотреть систему:
- [B−1AB−1][xxs]=B−1b{\displaystyle {\begin{bmatrix}B^{-1}A&B^{-1}\end{bmatrix}}{\begin{bmatrix}x\\x_{s}\end{bmatrix}}=B^{-1}b}
При фиксированных значениях небазисных переменных система однозначно разрешима относительно базисных, поэтому мы можем определить, какая из базисных переменных первой достигнет нуля при увеличении входящей. Эту переменную назовем выходящей. Это будет означать, что мы натолкнулись на новую вершину. Теперь входящую и выходящую переменную поменяем местами — входящая «войдёт» в базисную, а выходящая из них «выйдет» в небазисные. Теперь перепишем матрицу B и вектор cB в соответствии с новыми наборами базисных и небазисных переменных, после чего вернёмся ко второму шагу. x''
Поскольку число вершин конечно, то алгоритм однажды закончится. Найденная вершина будет являться оптимальным решением.
Причины использования[править | править код]
Если в условии задачи линейного программирования не все ограничения представлены неравенствами типа «≤», то далеко не всегда нулевой вектор будет допустимым решением. Однако каждая итерация симплекс-метода является переходом от одной вершины к другой, и если неизвестно ни одной вершины, алгоритм вообще не может быть начат.
Процесс нахождения исходной вершины не сильно отличается от однофазного симплекс-метода, однако может в итоге оказаться сложнее, чем дальнейшая оптимизация.
Модификация ограничений[править | править код]
Все ограничения задачи модифицируются согласно следующим правилам:
- ограничения типа «≤» переводятся на равенства созданием дополнительной переменной с коэффициентом «+1». Эта модификация проводится и в однофазном симплекс-методе, дополнительные переменные в дальнейшем используются как исходный базис.
- ограничения типа «≥» дополняются одной переменной с коэффициентом «−1». Поскольку такая переменная из-за отрицательного коэффициента не может быть использована в исходном базисе, необходимо создать ещё одну, вспомогательную, переменную. Вспомогательные переменные всегда создаются с коэффициентом «+1».
- ограничения типа «=» дополняются одной вспомогательной переменной.
Соответственно, будет создано некоторое количество дополнительных и вспомогательных переменных. В исходный базис выбираются дополнительные переменные с коэффициентом «+1» и все вспомогательные. Осторожно: решение, которому соответствует этот базис, не является допустимым.
Различия между дополнительными и вспомогательными переменными[править | править код]
Несмотря на то, что и дополнительные, и вспомогательные переменные создаются искусственно и используются для создания исходного базиса, их значения в решении сильно отличаются:
- дополнительные переменные сообщают, насколько соответствующее им ограничение «недоиспользовано». Значение дополнительной переменной, равное нулю, соответствует равенству значений правых и левых частей ограничения.
- вспомогательные переменные сообщают, насколько данное условие далеко от допустимого (относительно конкретного ограничения). Если значение вспомогательной переменной больше нуля, то данное решение не выполняет определённое ограничение, а значит не является допустимым.
То есть ненулевое значение дополнительной переменной может (но не должно) сигнализировать о неоптимальности решения. Ненулевое значение вспомогательной переменной сигнализирует о недопустимости решения.
Фазы решения[править | править код]
После того, как было модифицировано условие, создаётся вспомогательная целевая функция. Если вспомогательные переменные были обозначены, как yi{\displaystyle y_{i}}, i∈{1,…,k}{\displaystyle i\in \left\{1,\dots ,k\right\}}, то вспомогательную функцию определим, как
После этого проводится обыкновенный симплекс-метод относительно вспомогательной целевой функции. Поскольку все вспомогательные переменные увеличивают значение z′{\displaystyle z'}, в ходе алгоритма они будут поочерёдно выводится из базиса, при этом после каждого перехода новое решение будет всё ближе к множеству допустимых решений.
Когда будет найдено оптимальное значение вспомогательной целевой функции, могут возникнуть две ситуации:
- оптимальное значение z′{\displaystyle z'} больше нуля. Это значит, что как минимум одна из вспомогательных переменных осталась в базисе. В таком случае можно сделать вывод, что допустимых решений данной задачи линейного программирования не существует.
- оптимальное значение z′{\displaystyle z'} равно нулю. Это означает, что все вспомогательные переменные были выведены из базиса, и текущее решение является допустимым.
Во втором случае мы имеем допустимый базис, или, иначе говоря, исходное допустимое решение. Можно проводить дальнейшую оптимизацию с учётом исходной целевой функции, при этом уже не обращая внимания на вспомогательные переменные. Это и является второй фазой решения.
В модифицированном методе матрица
[1cBTB−1A−cTcBTB−10B−1AB−1]{\displaystyle {\begin{bmatrix}1&c_{B}^{T}B^{-1}A-c^{T}&c_{B}^{T}B^{-1}\\0&B^{-1}A&B^{-1}\end{bmatrix}}}
не пересчитывается, хранится и пересчитывается только матрица B−1{\displaystyle B^{-1}}. В остальном алгоритм похож на вышеописанный.
1. Вычисляем двойственные переменные d=cBTB−1{\displaystyle d=c_{B}^{T}B^{-1}}
2. Проверка оптимальности. cBTB−1A−cT{\displaystyle c_{B}^{T}B^{-1}A-c^{T}} преобразуется в dTA−cT{\displaystyle d^{T}A-c^{T}}.
Проверка заключается в вычислении dTAn−cn{\displaystyle d^{T}A_{n}-c_{n}} для всех столбцов n∈N{\displaystyle n\in N}. Столбец со значением < 0 можно вводить в базис.
Часто выбирают минимальное значение, но для этого нужно перебрать все столбцы.
Чаще выбирают значение, меньшее некоторого заданного значения −ε{\displaystyle -\varepsilon }
Если такого столбца не обнаружится, за ε{\displaystyle \varepsilon } принимается максимальное найденное абсолютное значение и соответствующий столбец AJ{\displaystyle A_{J}} вводится в базис.
3. Определение выводимого.
Пусть AJ{\displaystyle A_{J}} — вводимый столбец, соответствующий переменной xJ{\displaystyle x_{J}} Базисный план — это решение системы ABp=b{\displaystyle A_{B}p=b} Увеличиваем ABp+ϑAJ=b{\displaystyle A_{B}p+\vartheta A_{J}=b}.
Умножим слева на B−1{\displaystyle B^{-1}}, то есть B−1ABp+ϑB−1AJ=B−1b{\displaystyle B^{-1}A_{B}p+\vartheta B^{-1}A_{J}=B^{-1}b}.
Здесь B−1b{\displaystyle B^{-1}b} — базисный план, q=B−1AJ{\displaystyle q=B^{-1}A_{J}} — разложение вводимого столбца по базису.
Находим максимальное значение ϑ{\displaystyle \vartheta }, при котором все значения не отрицательны. Если ϑ{\displaystyle \vartheta } может быть взято как угодно велико, решение не ограничено. В противном случае один из элементов выйдет на нулевое значение. Выводим соответствующий столбец из базиса.
4. Пересчет опорного(базисного) плана.
Вычисляем новый опорный план по уже приведенной формуле x=p+ϑB−1AJ{\displaystyle x=p+\vartheta B^{-1}A_{J}} с найденным значением ϑ{\displaystyle \vartheta }.
5. Пересчитываем обратную к базисной B−1{\displaystyle B^{-1}}.
Пусть B−1AF{\displaystyle B^{-1}A_{F}} — выводимый столбец.
Матрица B представима в виде [BGAF]{\displaystyle [B_{G}A_{F}]}
где BG{\displaystyle B_{G}} — базисная матрица без выводимого столбца.
После замены столбца базисная матрица будет иметь вид [BGAJ]{\displaystyle [B_{G}A_{J}]}
Нам нужно найти матрицу B1{\displaystyle B_{1}}, такую что
[BG,AJ]B1−1=E{\displaystyle [B_{G},A_{J}]B_{1}^{-1}=E} => [B−1BGB1−1,B−1AJ]=B−1{\displaystyle [B^{-1}B_{G}B_{1}^{-1},B^{-1}A_{J}]=B^{-1}} => [B−1BG,q]B1−1=B−1{\displaystyle [B^{-1}B_{G},q]B_{1}^{-1}=B^{-1}} =>
[Eq′0qf]B1−1=B−1{\displaystyle {\begin{bmatrix}E&q'\\0&q_{f}\end{bmatrix}}B_{1}^{-1}=B^{-1}}
Откуда B1−1=[E−q′/qf01/qf]B−1{\displaystyle B_{1}^{-1}={\begin{bmatrix}E&-q'/q_{f}\\0&1/q_{f}\end{bmatrix}}B^{-1}}
Замечание.
При пересчете матрицы B−1{\displaystyle B^{-1}} накапливаются ошибки округления. Во избежание получения больших ошибок время от времени матрица пересчитывается полностью. Этот процесс называется «повторением».
Мультипликативный вариант симплекс-метода[править | править код]
В мультипликативном варианте матрица B−1{\displaystyle B^{-1}} не хранится, хранятся лишь множители [E−q′/qf01/qf]{\displaystyle {\begin{bmatrix}E&-q'/q_{f}\\0&1/q_{f}\end{bmatrix}}}
При решении экономических задач часто матрица ограничений разреженная, в таком случае мультипликативный вариант получает дополнительные преимущества — можно хранить мультипликаторы в сжатом виде (не хранить нули).
Во избежание накопления ошибок округления может использоваться LU-разложение матрицы.
При подавляющем числе ограничений типа «неравенство» может быть использован метод переменного базиса. [4]
Метод основан на том, что базисная матрица может быть представлена в виде
[AB0AEE]{\displaystyle {\begin{bmatrix}A_{B}&0\\A_{E}&E\end{bmatrix}}}
Обратная к ней имеет вид
[AB−10−AB−1AEE]{\displaystyle {\begin{bmatrix}A_{B}^{-1}&0\\-A_{B}^{-1}A_{E}&E\end{bmatrix}}}
При относительно небольших размерах матрицы AB−1{\displaystyle A_{B}^{-1}} остальная часть матрицы может не храниться.
Таким подходом удается решить задачи с десятками миллионов строк ограничений (например, из теории игр).
Для реализации двойственного метода необходимо перейти от задачи на минимум к задаче на максимум (или наоборот) путём транспонирования матрицы коэффициентов. При переходе от задачи на минимум целевая функция примет вид:
g=∑i=1nbiyi→max{\displaystyle g=\sum _{i=1}^{n}b_{i}y_{i}\to max}
при ограничениях
∑i=1naijyi≤cj{\displaystyle \sum _{i=1}^{n}a_{ij}y_{i}\leq c_{j}}.
Теорема двойственности. Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причем экстремальные значения линейных функций этих задач равны.
Если линейная функция одной из задач не ограничена, то другая не имеет решения.
Симплекс-метод удивительно эффективен на практике, но в 1972 Кли и Минти [5] привели пример, в котором симплекс-метод перебирал все вершины симплекса, что показывает экспоненциальную сходимость
симплекс — Викисловарь
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | си́мплекс | си́мплексы |
| Р. | си́мплекса | си́мплексов |
| Д. | си́мплексу | си́мплексам |
| В. | си́мплекс | си́мплексы |
| Тв. | си́мплексом | си́мплексами |
| Пр. | си́мплексе | си́мплексах |
си́мплекс
Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).
Корень: -симплекс- [Тихонов, 1996].
Произношение[править]
Семантические свойства[править]
Значение[править]
- геометр. N-мерный тетраэдр ◆ Основные координатные фигуры (точка, отрезок линии, треугольник, тетраэдр, пентатоп и т. д.) остова Н. С. Курнаков называет координатными симплексами. А.А. Щепеткин, Н.С. Курнаков, «Физико-химический анализ оксидов на основе металлов переменной валентности», 1987 г.
- в телекоммуникации односторонняя передача данных ◆ Отсутствует пример употребления (см. рекомендации).
- лингв. простая по структуре языковая единица (односложное слово, форма простого глагольного сказуемого, простая форма степеней сравнения, простое предложение и прочее)
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
- тетраэдр
Гипонимы[править]
Родственные слова[править]
Этимология[править]
Происходит от ??
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
| Список переводов | |
Библиография[править]
Симплекс - это... Что такое Симплекс?
(математический), простейший выпуклый многогранник данного числа измерений n. При n = 3 трёхмерный С. представляет собой произвольный, в том числе неправильный, тетраэдр. Под двумерным С. понимают произвольный треугольник, а под одномерным — отрезок. Нульмерный С. есть просто одна точка.
n-мерный С. имеет n + 1 вершин, не принадлежащих ни к какому (n — 1)-мерному подпространству того евклидова пространства (с числом измерений n или больше), в котором лежит данный С. Обратно, всякие n + 1 точек евклидова n-мерного пространства Rm, m ≥ n, не лежащие ни в каком подпространстве менее n измерений, однозначно определяют n-mepный С. с вершинами в заданных точках e0, e1,..., en, он может быть определён как выпуклое замыкание совокупности заданных n + 1 точек, т. е. как пересечение всех выпуклых тел пространства Rm, содержащих эти точки. Если в пространстве Rm дана система декартовых координат x1, х2,..., хт, в которой вершина ei, i = 0, 1,..., n, имеет координаты x1(i), x2(i),..., xm (i), то С. с вершинами e0, e1,..., em состоит из всех точек пространства, координаты которых имеют вид:
, k = 1,2,..., m, где μ(0), μ(1),..., μ(n) — произвольные неотрицательные числа, дающие в сумме 1. По аналогии со случаем n ≤ З можно сказать, что все точки С. с данными вершинами получаются, если в эти вершины поместить произвольные неотрицательные массы (из которых по крайней мере одна отлична от нуля) и взять центр тяжести этих масс (дополнительное требование, чтобы сумма всех масс равнялась 1, исключает лишь случай, когда все массы — нулевые).
Любые r + 1 вершин, 0 ≤ r ≤ n — 1, взятые из числа данных n + 1 вершин n-мерного С., определяют некоторый r-мерный С. — r-мерную грань данного С. Нульмерные грани С. суть его вершины, одномерные грани называются ребрами.
Лит.: Александров П. С., Комбинаторная топология, М. — Л., 1947; Понтрягин Л. С., Основы комбинаторной топологии, М. — Л., 1947, с. 23—31.
Подробный разбор симплекс-метода / Habr
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
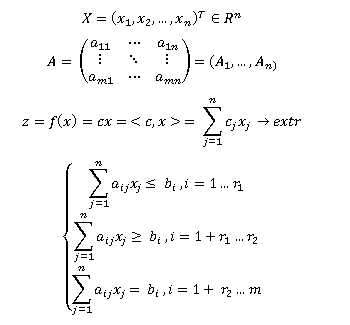
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными $inline$b_i$inline$ умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем $inline$s_i$inline$ – добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем $inline$s_i$inline$, и получаем равенство.
- Делаем замену переменных:
- Если $inline$x_i ≤ 0$inline$, то $inline$x_i'= -x_i ≥ 0$inline$
- Если $inline$x_i$inline$ — любой, то $inline$x_i= x_i' - x_i''$inline$, где $inline$x_i', x_i''≥ 0$inline$
Замечание: Будем нумеровать $inline$s_i$inline$ по номеру неравенства, в которое мы его добавили.
Замечание: $inline$s_i$inline$ ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение: Точка $inline$Х ∈ D$inline$ называется угловой точкой, если представление$inline$ Х= αХ^1+ (1-α) Х^2,где Х^1,Х^2 ∈D;0< α<1 $inline$ возможно только при $inline$Х^1=Х^2 $inline$.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит $inline$Х$inline$ (т.е. $inline$Х$inline$ – не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
Необходимые условия для применения симплекс-метода:
- Задача должна иметь каноническую форму.
- У задачи должен быть явно выделенный базис.
Определение: Явно выделенным базисом будем называть вектора вида:$inline$(..0100..)^T, (..010..)^T,(..0010..)^T...$inline$, т.е. только одна координата вектора ненулевая и равна 1.
Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание: Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание: Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.
Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение: Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение: Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание: Преобразование такого вида направлено на введение выбранной переменной в базис, т.е. представление ведущего столбца в виде базисного вектора.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.
Слово СИМПЛЕКС - Что такое СИМПЛЕКС?
Слово состоит из 8 букв: первая с, вторая и, третья м, четвёртая п, пятая л, шестая е, седьмая к, последняя с,
Слово симплекс английскими буквами(транслитом) - simpleks
Значения слова симплекс. Что такое симплекс?
Симплекс
Симплекс (от лат. simplex — простой) (математический), простейший выпуклый многогранник данного числа измерений n. При n = 3 трёхмерный С. представляет собой произвольный, в том числе неправильный, тетраэдр.
БСЭ. — 1969—1978
Симплекс [simplex] — выпуклый многоугольник в n-мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости. С. выделены в отдельный класс потому, что в n-мерном пространстве n точек всегда лежат в одной гиперплоскости.
slovar-lopatnikov.ru
СИМПЛЕКС [simplex] — выпуклый многоугольник в n-мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости. С. выделены в отдельный класс потому, что в n-мерном пространстве n точек всегда лежат в одной гиперплоскости.
Лопатников. — 2003
Саб симплекс
Саб симплекс Способ применения и дозы: Внутрь, во время или после еды и, при необходимости, перед сном. Перед применением следует активно встряхнуть флакон. Чтобы суспензия начала поступать из пипетки…
РЛС. — 2012
Саб симплексДействующее вещество ›› Симетикон* (Simethicone*) Латинское название Sab simplex АТХ:›› A02DA Ветрогонные препараты Фармакологическая группа…
Словарь медицинских препаратов. - 2005
САБ® СИМПЛЕКС (SAB® SIMPLEX) Суспензия для приема внутрь от белого до серо-белого цвета, слегка вязкая, с характерным фруктовым (ванильно-малиновым) запахом. 100 мл симетикон 6.919 г…
Справочник лекарственных препаратов "Видаль"
ШОКЕ СИМПЛЕКС
ШОКЕ СИМПЛЕКС - непустое компактное выпуклое множество Xв локально выпуклом пространстве E, обладающее следующим свойством: при вложении Ев качестве гиперплоскости в пространство проектирующий конус.
Математическая энциклопедия. - 1977-1985
Шеффилд-Симплекс
«Шеффилд-Симплекс» (англ. Sheffield-Simplex) — лёгкий пулемётный бронеавтомобиль Вооружённых сил Российской империи. Разработан британской фирмой «Sheffield-Simplex» на базе шасси собственного легкового автомобиля...
ru.wikipedia.org
Нордитропин Симплекс
Нордитропин Симплекс Показания: Задержка роста у детей вследствие недостаточности гормона роста или хронической почечной недостаточности (в препубертатном возрасте), синдрома Шерешевского — Тернера…
РЛС. — 2012
НОРДИТРОПИН® СИМПЛЕКС® (NORDITROPIN SimpleXx) Раствор для п/к введения 1.5 мл (1 картридж) соматропин 10 мг 1.5 мл - картриджи (1) - упаковки ячейковые контурные (1) - пачки картонные.
Справочник лекарственных препаратов "Видаль"
СТАНДАРТНЫЙ СИМПЛЕКС
СТАНДАРТНЫЙ СИМПЛЕКС - 1) С. с.- симплекс размерности пв пространстве с вершинами в точках е i=(0,…, 1,…, 0), i=0,…, п(единица стоит на i-м месте), т. е.
Математическая энциклопедия. - 1977-1985
Двойственный симплекс-метод
Двойственный симплекс-метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами. В обычном симплексном алгоритме план всегда должен быть допустимым.
ru.wikipedia.org
Русский язык
Си́мпле́кс/.
Морфемно-орфографический словарь. — 2002
- симпатяга
- симпласт
- симплексный
- симплекс
- симплока
- симподий
- симпозиум
СИМПЛЕКС - это... Что такое СИМПЛЕКС?
- топологическое пространство | А|, точками к-рого служат неотрицательные функции , определенные на конечном множестве Аи удовлетворяющие условию . Топология в | А| полагается индуцированной из - пространства всех функций из Ав . Действительное число j(а) наз. а-й барицентрической координатой точки j, размерностью симплекса | А| наз. число car dA-1. В случае, когда Аявляется линейно независимым подмножеством евклидова пространства, симплекс | А| гомеоморфен выпуклой оболочке множества А(гомеоморфизм задается соответствием ). В связи с этим выпуклая оболочка линейно независимого подмножества евклидова пространства наз. евклидовым С.
Для любого отображения конечных множеств формула , определяет непрерывное отображение , являющееся для евклидовых С.
аффинным (неоднородным линейным) отображением, продолжающим отображение f. Этим задается функтор из категории конечных множеств в категорию топологич. пространств. Если и - соответствующее вложение, то |i| - гомеоморфизм на замкнутое подмножество, наз. гранью симплекса | А| и обычно отождествляемое с |В|. Нульмерные грани наз. вершинами (как правило, вершины отождествляются с элементами множества А).
Топологическим упорядоченным С. наз. топологич. пространство X, для к-рого задан гомеоморфизм , где Dn - стандартный симплекс. Образ граней Dn при гомеоморфизме hназ. гранью топологического упорядоченного симплекса X. Отображение топологических упорядоченных симплексов Xи Yназ. линейным, если оно имеет вид , где kи h - заданные гомеоморфизмы, F - произвольное отображение вида |f|.
Топологическим С. (размерности n) наз. топологич. пространство X, наделенное (n+1)! гомеоморфизмами (то есть (n+1)! структурами топологического упорядоченного С.), отличающимися на гомеоморфизмы вида |f|, где f - произвольная перестановка вершин. Аналогично, отображение топологического С. наз. линейным, если оно является линейным отображением соответствующих топологических упорядоченных С.
С. наз. также элементы симплициальных множеств и отмеченные подмножества симплициальных схем.
А. В. Хохлов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
симплекс - это... Что такое симплекс?
симплекс — симплексное соединение — [http://www.iks media.ru/glossary/index.html?glossid=2400324] симплекс Выпуклый многоугольник в n мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости. С. выделены в отдельный класс потому, что в… … Справочник технического переводчика
симплекс — сущ., кол во синонимов: 1 • многогранник (38) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Симплекс — [simplex] выпуклый многоугольник в n мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости. С. выделены в отдельный класс потому, что в n мерном пространстве n точек всегда лежат в одной гиперплоскости. Так что С. это простейший … Экономико-математический словарь
Симплекс — * сімплекс * simplex автотетраплоид, в генотипе которого один аллель из четырех является доминантным: Аааа () … Генетика. Энциклопедический словарь
Симплекс — Запрос «Симплекс» перенаправляется сюда; см. также другие значения. Симплекс или n мерный тетраэдр (от лат. simplex простой) геометрическая фигура, являющаяся n мерным обобщением треугольника. Содержание 1 Определение … Википедия
СИМПЛЕКС — топологическое пространство | А|, точками к рого служат неотрицательные функции , определенные на конечном множестве Аи удовлетворяющие условию . Топология в | А| полагается индуцированной из пространства всех функций из Ав . Действительное число … Математическая энциклопедия
СИМПЛЕКС — re мерный многогранник, являющийся выпуклой оболочкой n+1 точек (вершин С.), к рые не лежат в ( п 1) мерной плоскости. При n=0, 1, 2, 3 С. точка, отрезок, треугольник, тетраэдр. Грани С. суть С. меньшей размерности. Два С. одинаковой размерности… … Математическая энциклопедия
симплекс — simplex симплекс. Генотипический класс аутотетраплоидного организма, у которого данный диаллельный ген имеет конституцию Aaaa. (Источник: «Англо русский толковый словарь генетических терминов». Арефьев В.А., Лисовенко Л.А., Москва: Изд во ВНИРО,… … Молекулярная биология и генетика. Толковый словарь.
симплекс — pakaitinis dvipusis ryšys statusas T sritis automatika atitikmenys: angl. simplex vok. Wechselschreiben, n; Wechselsprechen, n rus. симплекс, m pranc. simplex, n ryšiai: sinonimas – simpleksinis ryšys … Automatikos terminų žodynas
симплекс — simpleksas statusas T sritis augalininkystė apibrėžtis Autotetraploidas, kurio genotipe tik vienas geno alelis iš keturių yra vyraujantis. atitikmenys: angl. simplex rus. симплекс … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas
Симплекс — Большая советская энциклопедия
Симпле́кс
(от лат. simplex — простой)
(математический), простейший выпуклый многогранник данного числа измерений n. При n = 3 трёхмерный С. представляет собой произвольный, в том числе неправильный, тетраэдр. Под двумерным С. понимают произвольный треугольник, а под одномерным — отрезок. Нульмерный С. есть просто одна точка.
n-мерный С. имеет n + 1 вершин, не принадлежащих ни к какому (n — 1)-мерному подпространству того евклидова пространства (с числом измерений n или больше), в котором лежит данный С. Обратно, всякие n + 1 точек евклидова n-мерного пространства Rm, m ≥ n, не лежащие ни в каком подпространстве менее n измерений, однозначно определяют n-mepный С. с вершинами в заданных точках e0, e1,..., en, он может быть определён как выпуклое замыкание совокупности заданных n + 1 точек, т. е. как пересечение всех выпуклых тел пространства Rm, содержащих эти точки. Если в пространстве Rm дана система декартовых координат x1, х2,..., хт, в которой вершина ei, i = 0, 1,..., n, имеет координаты x1(i), x2(i),..., xm (i), то С. с вершинами e0, e1,..., em состоит из всех точек пространства, координаты которых имеют вид:
, k = 1,2,..., m, где μ(0), μ(1),..., μ(n) — произвольные неотрицательные числа, дающие в сумме 1. По аналогии со случаем n ≤ З можно сказать, что все точки С. с данными вершинами получаются, если в эти вершины поместить произвольные неотрицательные массы (из которых по крайней мере одна отлична от нуля) и взять центр тяжести этих масс (дополнительное требование, чтобы сумма всех масс равнялась 1, исключает лишь случай, когда все массы — нулевые).
Любые r + 1 вершин, 0 ≤ r ≤ n — 1, взятые из числа данных n + 1 вершин n-мерного С., определяют некоторый r-мерный С. — r-мерную грань данного С. Нульмерные грани С. суть его вершины, одномерные грани называются ребрами.
Лит.: Александров П. С., Комбинаторная топология, М. — Л., 1947; Понтрягин Л. С., Основы комбинаторной топологии, М. — Л., 1947, с. 23—31.
Источник: Большая советская энциклопедия на Gufo.me
Значения в других словарях
- симплекс — Симплекс, симплексы, симплекса, симплексов, симплексу, симплексам, симплекс, симплексы, симплексом, симплексами, симплексе, симплексах Грамматический словарь Зализняка
- симплекс — орф. симплекс, -а Орфографический словарь Лопатина
- симплекс — Си́мпле́кс/. Морфемно-орфографический словарь
- симплекс — сущ., кол-во синонимов: 1 многогранник 38 Словарь синонимов русского языка
- Симплекс — Re-мерный многогранник, являющийся выпуклой оболочкой n+1 точек (вершин С.), к-рые не лежат в ( п-1)-мерной плоскости. При n=0, 1, 2, 3 С.- точка, отрезок, треугольник, тетраэдр. Грани С. суть С. меньшей размерности. Два... Математическая энциклопедия
Правильный 9-симплекс — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 сентября 2017; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 сентября 2017; проверки требуют 3 правки.Правильный 9-симплекс, или декаиоттон, или дека-9-топ — правильный самодвойственный девятимерный политоп. Имеет 10 вершин, 45 рёбер, 120 граней, имеющих форму правильного треугольника, 210 правильнотетраэдрических ячеек, 252 пятиячейниковых 4-ячейки, 210 5-ячеек, имеющих форму правильного 5-симплекса, 120 6-ячеек, имеющих форму правильного 6-симплекса, 45 7-ячеек, имеющих форму правильного 7-симплекса и 10 8-ячеек, имеющих форму правильного 8-симплекса. Его двугранный угол равен arccos(1/9), то есть примерно 83,62°.
Правильный 9-сипмлекс можно разместить в Декартовой системе координат следующим образом (длина ребра тела равна 2 и центр приходится на начало координат):
- (1/45, 1/6, 1/28, 1/21, 1/15, 1/10, 1/6, 1/3, ±1){\displaystyle \left({\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)}
- (1/45, 1/6, 1/28, 1/21, 1/15, 1/10, 1/6, −21/3, 0){\displaystyle \left({\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)}
- (1/45, 1/6, 1/28, 1/21, 1/15, 1/10, −3/2, 0, 0){\displaystyle \left({\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)}
- (1/45, 1/6, 1/28, 1/21, 1/15, −22/5, 0, 0, 0){\displaystyle \left({\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)}
- (1/45, 1/6, 1/28, 1/21, −5/3, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)}
- (1/45, 1/6, 1/28, −12/7, 0, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)}
- (1/45, 1/6, −7/4, 0, 0, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/45}},\ 1/6,\ -{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
- (1/45, −4/3, 0, 0, 0, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/45}},\ -4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
- (−31/5, 0, 0, 0, 0, 0, 0, 0, 0){\displaystyle \left(-3{\sqrt {1/5}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
Правильный 10-симплекс — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 июня 2017; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 июня 2017; проверки требуют 3 правки.| Правильный 10-симплекс | |
|---|---|
 | |
| Тип | Правильный десятимерный политоп |
| Символ Шлефли | {3,3,3,3,3,3,3,3,3} |
| 9-мерных ячеек | 11 |
| 8-мерных ячеек | 55 |
| 7-мерных ячеек | 165 |
| 6-мерных ячеек | 330 |
| 5-мерных ячеек | 462 |
| 4-мерных ячеек | 462 |
| Ячеек | 330 |
| Граней | 165 |
| Рёбер | 55 |
| Вершин | 11 |
| Вершинная фигура | Правильный 9-симплекс |
| Двойственный политоп | Он же (самодвойственный) |
Правильный 10-симплекс, или гендекаксеннон, или гендека-10-топ — правильный самодвойственный десятимерный политоп. Имеет 11 вершин, 55 рёбер, 165 граней - правильных треугольников, 330 правильнотетраэдрических ячеек, 462 пятиячейниковых 4-ячейки, 462 5-ячейки, имеющих форму правильного 5-симплекса, 330 6-ячеек, имеющих форму правильного 6-симплекса, 165 7-ячеек, имеющих форму правильного 7-симплекса, 55 8-ячеек, имеющих форму правильного 8-симплекса и 11 9-ячеек, имеющих форму правильного 9-симплекса. Его двугранный угол равен arccos(0,1), то есть примерно 84,26°.
Правильный 10-сипмлекс можно разместить в Декартовой системе координат следующим образом (длина ребра тела равна 2 и центр приходится на начало координат):
- (1/55, 1/45, 1/6, 1/28, 1/21, 1/15, 1/10, 1/6, 1/3, ±1){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)}
- (1/55, 1/45, 1/6, 1/28, 1/21, 1/15, 1/10, 1/6, −21/3, 0){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)}
- (1/55, 1/45, 1/6, 1/28, 1/21, 1/15, 1/10, −3/2, 0, 0){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)}
- (1/55, 1/45, 1/6, 1/28, 1/21, 1/15, −22/5, 0, 0, 0){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)}
- (1/55, 1/45, 1/6, 1/28, 1/21, −5/3, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)}
- (1/55, 1/45, 1/6, 1/28, −12/7, 0, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)}
- (1/55, 1/45, 1/6, −7/4, 0, 0, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ -{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
- (1/55, 1/45, −4/3, 0, 0, 0, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ -4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
- (1/55, −31/5, 0, 0, 0, 0, 0, 0, 0, 0){\displaystyle \left({\sqrt {1/55}},\ -3{\sqrt {1/5}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
- (−20/11, 0, 0, 0, 0, 0, 0, 0, 0, 0){\displaystyle \left(-{\sqrt {20/11}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}